An Advanced Team-Based Rating System

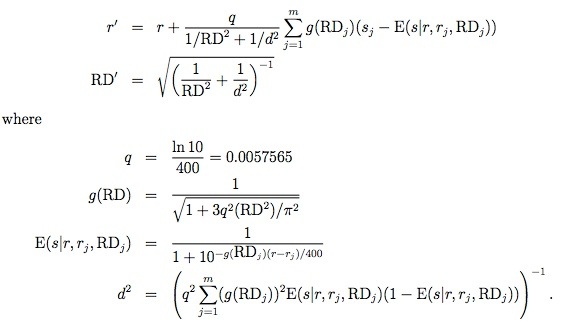
The Problem with Existing Systems

Rating systems like Elo and Glicko-2 are foundational to competitive matchmaking, from chess to video games. They excel at modeling 1v1 encounters where the outcome is a simple win, loss, or draw. However, when applied to modern team-based esports like Call of Duty or my own local Super Smash Bros. tournaments, their limitations become clear. I identified three core problems I wanted to solve:

1. Delayed Updates: Glicko-2 is designed to be updated in batches after a "rating period" of many games, making it unsuitable for live, game-by-game updates.
2. Team Dynamics: The systems are inherently player-vs-player and don't have a native way to handle team-based matchups where individual player ratings should contribute to a collective team strength.
3. Ignoring Performance: A win is a win, whether by a razor-thin margin or a complete blowout. Existing systems can't account for the *degree* of victory, losing valuable performance data in the process.

Engineering a Better Solution

My goal was to create an accurate, live, team-based rating system. This required a deep dive into the mathematics of Glicko-2 and developing novel adaptations to address each of its shortcomings.

1. Enabling Live, Per-Game Updates

The Glicko-2 formula involves summations over multiple games played within a rating period. To enable live updates, I re-engineered the core calculation (`rating_change` function) to operate on a single matchup. This involved "unrolling" the summations and modifying the update steps to process one game at a time, transforming it from a batch system into a real-time one.

2. Modeling Team-vs-Team Encounters

To handle team matchups, my system (`team_battle` function) calculates a temporary, aggregate rating for each team by averaging the ratings and rating deviations (RD) of its players. The rating update for each individual player is then calculated based on their performance against the *opposing team's average strength*. This method ensures that individual contributions are measured against the collective skill of their opponents, a crucial factor in team games with shifting rosters.

3. Incorporating Score and Margin of Victory

This was the most significant innovation. Instead of a binary win/loss (a score of 1 or 0), I needed to translate a raw game score (e.g., getting '3 stocked' in a game like Super Smash Ultimate) into a meaningful performance percentage. A simple ratio like `score / total_score` is flawed because winning the first point is statistically easier than winning the last point when the score is tied.

To solve this, I implemented a Binomial Cumulative Distribution Function (CDF). For each game and/or mode (like "Search and Destroy" or "Hardpoint"), the `bionomial_cdf` function calculates the true probability of winning the entire game given a certain score percentage. This `G` value (for "Game Outcome") becomes the new "score" fed into the Glicko-2 formula. A dominant 4-0 victory now results in a `G` value close to 1.0, while a close 4-3 win results in a `G` value much closer to 0.5, ensuring that dominant victories are rewarded more significantly. This can all memoized for performance.

Results and Application

The resulting system is a significant improvement over standard Glicko-2 for its intended purpose. It provides more stable, accurate, and responsive ratings that reflect not just if a team won, but *how* they won. This system is currently live and in use for ranking my local Super Smash Bros. group, demonstrating its practical application and effectiveness.